Según la tradición, las secciones cónicas fueron descubiertas por el geómetra y matemático griego Menecmo (380 A. C.- 320 A. C.), en su estudio del problema de la duplicación del cubo, mediante el cual demostró la existencia de una solución usando el corte de una parábola con una hipérbola, lo cual es confirmado posteriormente por los también geómetras Proclo y Eratóstenes.
Sin embargo, el primero en usar el término hipérbola fue Apolonio de Perge en su tratado Cónicas, considerada la obra cumbre sobre el tema de las matemáticas griegas, y donde se desarrolla el estudio de las tangentes a las secciones cónicas.
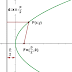
La hipérbola es una curva plana, abierta, con dos ramas; se define como el lugar geométrico de los puntos cuya diferencia de distancias a otros dos fijos, llamados focos, es constante e igual a 2a = AB, la longitud del eje real. Tiene dos ejes perpendiculares que se cortan en el punto medio O, centro de la curva.
ELEMENTOS DE LA HIPERBOLA
- Focos: Son los puntos fijos F y F.
- Eje focal, principal o real: Es la recta que pasa por los focos.
- Eje secundario o imaginario: Es la mediatriz del segmento FF.
- Centro: Es el punto de intersección de los ejes.
- Vértices: Los puntos A y A son los puntos de intersección de la hipérbola con el eje focal.
- Radios vectores: Son los segmentos que van desde un punto de la hipérbola a los focos: PF y PF.
- Distancia focal: Es el segmento FF de longitud 2C.
- Eje mayor: Es el segmento AA de longitud 2A.
- Eje menor: Es el segmento BB de longitud 2B.
- Los puntos B y B se obtienen como intersección del eje imaginario con la circunferencia que tiene por centro uno de los vértices y de radio C.
- Ejes de simetría: Son las rectas que contienen al eje real o al eje imaginario.
- Asintotas: Son las rectas de ecuaciones:

- Relación entre los semiejes:

ENCUESTA DE LA HIPERBOLA

.svg.png)

.jpeg)
.svg.png)
No hay comentarios.:
Publicar un comentario