PROPIEDADES DE LA PARÁBOLA
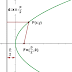
Se define como el lugar geométrico de los puntos del plano que equidistan de un punto fijo F, llamado foco, y de una recta fija d, llamada directriz. Tiene un vértice v y un eje de simetría que pasa por v y por el foco y es perpendicular a la directriz. La tangente en el vértice de la curva es paralela a la directriz.
El vértice, como otro punto cualquiera, equidista de la directriz y del foco, por lo tanto estará colocado en el punto medio del segmento AF.
La directriz d de la curva hace de circunferencia focal de la parábola, en este caso de radio infinito. Según esto, la directriz es el lugar geométrico de los puntos simétricos del foco respecto de cada tangente.
La tangente en el vértice, que es una recta, hace de circunferencia principal y se define como en las curvas anteriores.
.jpeg)
ELEMENTOS DE LA PARABOLA
- Foco: Es el punto fijo F.
- Directriz: Es la recta fija d.
- Parámetro: Es la distancia del foco a la directriz, se designa por la letra p.
- Eje: Es la recta perpendicular a la directriz que pasa por el foco.
- Vértice: Es el punto de intersección de la parábola con su eje.
- Radio vector: Es un segmento que une un punto cualquiera de la parábola con el foco.
Los elementos característicos de una parábola son: su eje o eje de simetría, el vértice (que corresponde con el máximo o mínimo de la parábola según sea su curvatura).
La ecuación de una parábola cuyo vértice es el (0,0) y su eje el eje de ordenadas.
.jpeg)
.svg.png)