AREA Y VOLUMEN DE UN PRISMA

El prisma es un tipo de poliedro formado por dos caras paralelas que son polígonos idénticos denominados bases. Estas figuras se unen por las caras laterales que son paralelogramos (cuadriláteros cuyos lados opuestos son paralelos).

            Elementos del prisma

Bases: Son dos polígonos paralelos e idénticos entre sí. Por ejemplo, dos cuadrados o dos pentágonos (como en la figura de abajo).

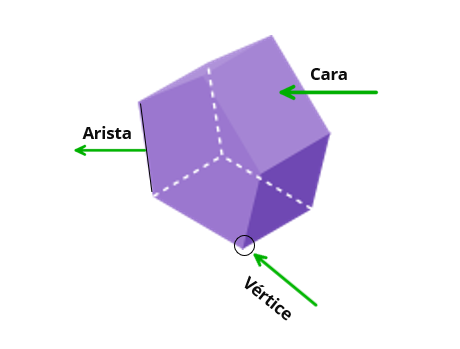
Caras laterales: Son paralelogramos que unen las dos bases. Pueden ser rectángulos, cuadrados, rombos o romboides. En la imagen inferior, el rectángulo ABJF es una de las caras laterales.

Aristas: Son los segmentos de recta que unen las caras del prisma. Por ejemplo, el segmento AB en el ejemplo de abajo.

Vértices: Es el punto donde coinciden tres caras del poliedro, como cualquiera de los puntos A, B, C, D, E, F, G, H, I o J en el prisma mostrado en la parte inferior.

Altura: La distancia que separa las dos bases de la figura. Si el prisma es recto, la altura es igual a la longitud de la arista de las caras laterales. Es decir, en el ejemplo de abajo, la altura mide igual que la arista AJ o BF.

Como vemos, este prisma hexagonal tiene 6 caras laterales que son rectángulos y 2 bases que son hexágonos.

El área lateral de un prisma es la suma de las áreas de sus caras laterales (los 6 rectángulos).

Las 6 caras laterales forman un rectángulo cuya base es el perímetro del hexágono de la base.

Por tanto, el área lateral del prisma es igual al producto del perímetro de la base por la altura:

Área lateral = perímetro de la base x altura

El área total es la suma del área lateral más el área de las 2 bases:

Área total = Área lateral + Área de la base x 2

El volumen del prisma recto, ortoedro, se calcula multiplicando las longitudes de las tres aristas convergentes a un vértice. Es lo que habitualmente llamamos largo, ancho y alto.

Volumen ortoedro = largo x ancho x alto

Por ejemplo, si las aristas de un prisma recto son 12, 5 y 5 cm, entonces

V = 12 cm x 5 cm x 5 cm = 300 cm³

Tipos de prisma

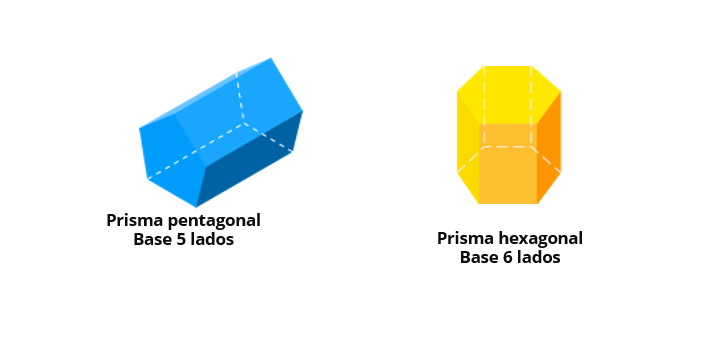
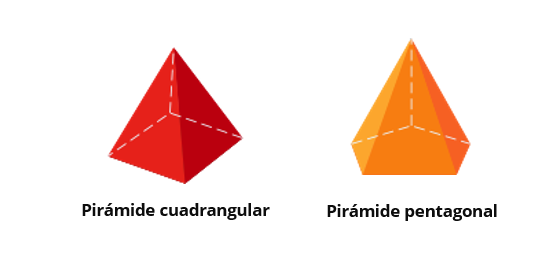
Los prismas pueden clasificarse en función a diferentes criterios. Primero, según el número de lados de sus bases, puede ser triangular, cuadrangular, pentagonal, hexagonal, etc.

Prisma triangular recto Prisma triangular oblicuo

Finalmente, se puede distinguir entre prismas convexos, cuando sus bases son polígonos convexos (todos los ángulos interiores de las caras son menores de 180º), y prismas cóncavos, cuando sus bases son polígonos cóncavos (al menos un ángulo interior de la base es mayor a 180º).

                                              Prisma convexo Prisma cóncavo   

AREA Y PERIMETRO DE UN CIRCULO

Recordamos los conceptos de círculo y circunferencia, proporcionamos las fórmulas y una calculadora del área y del perímetro y resolvemos algunos problemas.

Calculadora

Calculadora del área, AA, y perímetro, PP, de un círculo a partir de su radio, rr (no se admiten fracciones ni raíces).

                                    Perímetro y área

El perímetro de un círculo de radio rr es la longitud de su lado (borde):

Como el diámetro de un círculo es d=2⋅rd=2·r, podemos escribir el perímetro como

El área de un círculo es su superficie:

Ejemplo

Calculamos el área y el perímetro de un círculo de radio r=2 cmr=2 cm:

El área del círculo es 4π cm24π cm2 y el perímetro es 4π cm4π cm. Observad que ambas magnitudes son iguales, pero cambian las unidades de medida. Esto sólo ocurre cuando el radio es r=2r=2.

Circunferencia y círculo

¡El borde de un círculo es una circunferencia!

La circunferencia de radio r>0r>0 y centro c=(c1,c2)c=(c1,c2) es el lugar geométrico del plano formado por los puntos cuya distancia al punto cc es igual a rr.

Estos puntos (x,y)(x,y) son los que cumplen la ecuación

Representación:

Ejemplo

La circunferencia centrada en el origen c=(0,0)c=(0,0) y de radio r=1r=1 es

El círculo de radio r>0r>0 y centro c=(c1,c2)c=(c1,c2) es el lugar geométrico del plano formado por los puntos cuya distancia al punto cc es menor o igual que rr.

Estos puntos (x,y)(x,y) son los que cumplen la ecuación

Ejemplo

La circunferencia centrada en el origen c=(0,0)c=(0,0) y de radio r=1r=1 es

PROBABILIDAD Y ESTADISTICA 😎😎

Te explicamos qué son la probabilidad y la estadística, sus campos de estudio y características. Además, los tipos de estadística.

Cuando hablamos de probabilidad y estadística, nos referimos comúnmente al estudio del azar desde un punto de vista matemático. Es decir, al estudio de las leyes formales que lo rigen, desde dos puntos de vista claramente diferenciados:

La probabilidad se entiende como el grado de certidumbre que se posee respecto de que un evento ocurra o no, y constituye también una disciplina encargada de confeccionar modelos predictivos para fenómenos aleatorios, de modo de poder anticiparlos y estudiar sus consecuencias lógicas.

La estadística, en cambio, ofrece métodos y técnicas propios para comprender lo que dichos modelos significan, ya que es una disciplina independiente, rama de las matemáticas, centrada en el estudio de la variabilidad.

La probabilidad y la estadística se encuentran estrechamente vinculadas, dado que son las dos grandes herramientas de las que dispone la humanidad para enfrentarse a los fenómenos aleatorios.

Es decir, estudian aquellos cuyos patrones de ocurrencia escapan a nuestras perspectivas o implican cálculos demasiado grandes y con demasiado margen de error como para pretender abordarlos de manera concreta. Así, se impone la necesidad de hacer modelos y aproximaciones, y trabajar en términos de porcentajes de ocurrencia.

                       Probabilidad

La probabilidad es un campo de estudio, al cual se dedica la Teoría de la probabilidad, una rama de las matemáticas que se utiliza ampliamente en disciplinas como la matemática, las ciencias sociales, las finanzas, la economía y, claro está, la estadística, para obtener conclusiones respecto de qué tan probable es que un evento ocurra, o no ocurra.

La necesidad de este tipo de estudios surgió gracias al deseo del ser humano de poder predecir el futuro con cierto margen de certeza, algo que se traduce en la posibilidad de prever y evitar catástrofes, por ejemplo. Para ello propone diversas leyes y aproximaciones que permiten, a menudo, el cálculo científico de aquello que se considera probable, y que a menudo es contrario a lo que nuestra intuición nos señala.

                         Estadística

La estadística surgió de la mano de la necesidad del Estado moderno de pensar y controlar sus poblaciones crecientes. Esa es la razón de su nombre, prove
niente del italiano statista (“hombre de Estado”) y por traducción directa del alemán Statistik. En la actualidad, esta disciplina es útil para un sinfín de ciencias y aplicaciones, organizada en dos grandes áreas de estudio:

• Estadística descriptiva, dedicada a visualizar, describir y resumir numérica o gráficamente la información obtenida a partir de un conjunto de datos estadísticos.

• Estadística inferencial, dedicada a proponer modelos, predicciones e inferencias a partir de las observaciones hechas en torno a la aleatoriedad de un fenómeno.

Ambas ramas forman parte de la estadística aplicada, que aspira a resolver problemas sobre la probabilidad de ciertos asuntos reales. Algo vital para la toma de decisiones y la planificación futura.

TEOREMA DE PITAGORAS

En matemáticas, el teorema de Pitágoras es una relación en geometría euclidiana entre los tres lados de un triángulo rectángulo. Afirma que el área del cuadrado cuyo lado es la hipotenusa (el lado opuesto al ángulo recto) es igual a la suma de las áreas de los cuadrados cuyos lados son los catetos (los otros dos lados que no son la hipotenusa). Este teorema se puede escribir como una ecuación que relaciona las longitudes de los lados 'a', 'b' y 'c'. Es la proposición más conocida entre las que tienen nombre propio en la matemática. El teorema de Pitágoras establece que, en todo triángulo rectángulo, la longitud de la hipotenusa es igual a la raíz cuadrada de la suma del área de los cuadrados de las respectivas longitudes de los catetos.

El Teorema de Pitágoras es uno de los teoremas más célebres en el ámbito de las matemáticas y uno de los temas más temidos entre los estudiantes. No es casualidad que se trate de uno de los teoremas matemáticos más comunes, con el que nos seguimos topando incluso años después de haber salido de las instituciones educativas.

Este teorema se le atribuye a Pitágoras de Samos, nacido en 570 AC, sabio griego a quien debemos también la palabra filósofo

¿Qué establece el Teorema de Pitágoras? El Teorema de Pitágoras establece la relación existente entre los tres lados de un triángulo rectángulo.

En este artículo, te explicaremos de manera sencilla y práctica que es el Teorema de Pitágoras y te daremos algunos ejemplos, así que deja el miedo a un lado y adéntrate.

Para comenzar, es esencial aclarar algunos puntos importantes:Un triángulo es un polígono con tres lados;

Los ángulos de cualquier triángulo suman 180^o180o grados;

Un triángulo rectángulo es un triángulo en donde uno de los ángulos tiene 90 grados;

Un ángulo recto es un ángulo de 90 grados;

En todo triángulo rectángulo los lados adyacentes al ángulo recto reciben el nombre de catetos, es decir, los catetos son los lados que encierran el ángulo recto.

el lado más largo de un triángulo rectángulo, aquel que se opone al ángulo recto, recibe el nombre de hipotenusa.

¿Para qué se usa el Teorema de Pitágoras?

El Teorema de Pitágoras es, si se puede decir, la piedra fundacional de la geometría cartesiana, y por lo tanto se ha convertido en herramienta primordial en el desarrollo de las ciencias como las conocemos hoy día.

La importancia de este teorema proviene de la importancia del triángulo rectángulo, que es aquel triángulo que vincula la recta horizontal con la recta vertical (los catetos del triángulo). En efecto, la horizontal y la vertical siempre guardan entre sí un ángulo de 90^o90o, que es el mismo ángulo que encierran siempre entre sí los catetos del triángulo rectángulo.

El Teorema de Pitágoras tiene aplicación y es usado en todas las áreas de las ciencias, ya que todas tienen fundamento matemático.

Triángulo agudo
Triángulo obtuso
Triángulo escaleno
Triángulo equilátero
Triángulo isósceles

EXAMEN  TEOREMA DE PITAGORAS

ESTADISTICA DESCRIPTIVA E INFERENCIAL

QUE ES ESTADISTICA 

La definición de estadística ha adoptado muchas formas a lo largo de la historia. Hoy en día, se puede establecer como la ciencia que permite extraer información de los datos, así como la medición, el control, y la comunicación de la incertidumbre. Constituye, por tanto, la herramienta esencial para controlar el curso de los avances científicos y sociales.

La ciencia estadística ha ido aumentando el rango de técnicas, métodos y teorías que aglutinar, pero posiblemente la división más primaria que se puede hacer de la misma es la que distingue los campos de estadística descriptiva y estadística inferencial.

La estadística descriptiva tiene como objetivo resumir la información contenida en los datos de la forma más sencilla y presentable posible, obteniendo así los parámetros que distinguen las características de un conjunto de datos (lo que se conoce como estadísticos). Pertenecen al ámbito de la estadística descriptiva las tablas de frecuencias, a partir de las cuales se obtienen los estadísticos:

Medidas de centralización: la media en todas sus variantes (aritmética, geométrica, ponderada), la moda y la mediana

Medidas de dispersión: la varianza, la desviación típica (raíz cuadrada de la varianza) y el rango

Medidas de tendencia central: los cuantiles y sus desgloses (percentiles, cuartiles, deciles, etc.)

Medidas de forma: los coeficientes de asimetría y curtosis

Medidas de concentración: el coeficiente Gini, a partir del cual se obtiene la curva de Lorenz.

¿Qué es lo que distingue a la estadística descriptiva de la inferencial?

En primer lugar, la naturaleza de los datos. Mientras que la estadística descriptiva sirve tanto para una población como para una muestra (un subconjunto de esa población cuyos elementos son elegidos al azar), la estadística inferencial trabaja con muestras a partir de las cuales intenta extraer conclusiones sobre la población.

Esta práctica se conoce como inferir, y es importante recalcar la diferencia en la naturaleza de los datos, ya que es un error muy común el de extraer conclusiones de un conjunto cuyas conclusiones… son los mismos datos en sí.

Para explicar dicho error, conviene asimismo explicar la principal diferencia teórica entre estadística descriptiva e inferencial. La descriptiva, al ser únicamente una descripción de los datos, no asume que éstos tengan alguna propiedad más allá de las que se pueden describir con los estadísticos ya mencionados. En cambio, la inferencial asume que los datos se rigen bajo un fenómeno aleatorio subyacente que es el que hace que tomen un valor u otro. Es por esto por lo que los datos pasarían a denominarse variables aleatorias. Al existir incertidumbre, se puede igualmente describir la población de la que sale esa muestra, pero debemos entonces asumir un cierto error derivado de la naturaleza probabilística de los datos.

Un ejemplo práctico: si recogemos una muestra de alturas de 100 españoles, y obtenemos una media de 1,85, podemos asumir que es una variable aleatoria, y que por lo tanto, si la media de la muestra está en 1,85, es muy probable que la media de altura de todos los españoles esté en torno a esa cifra. Por otro lado, si hacemos un censo de las alturas de todos los habitantes de España, no hace falta asumir un riesgo o error para concluir con que la media es equivalente a una cifra concreta: al 100%, la media poblacional es la que obtenemos de ese censo.

OPERACIONES BASICAS😎😋

SUMA

Una suma (del latín summa) es el agregado de cosas. El término hace referencia a la acción y efecto de sumar o añadir. Aunque el concepto no siempre se encuentra relacionado con las matemáticas, a través de ellas puede comprenderse directa y claramente; en esta ciencia se entiende la suma como una operación que permite añadir una cantidad a otra u otras homogéneas. Como operación matemática, la suma o adhesión consiste en añadir dos números o más para obtener una cantidad total. El proceso también permite reunir dos grupos de cosas para obtener un único conjunto. Por ejemplo: si tengo tres manzanas y tomo otras dos, tendré cinco manzanas (3+2=5). Lo mencionado respecto a las cantidades homogéneas hace referencia a que, si a cinco manzanas le sumo cuatro peras, obtendré como resultado nueve, pero no nueve manzanas o nueve peras. La operación lógica es la misma (5+4=9), pero las cantidades no son homogéneas, a menos que se agrupen las manzanas y las peras en el conjunto de las frutas.

RESTA

La resta o sustracción es una operación matemática que se representa con el signo de restar o signo menos "-", y consiste en eliminar una cantidad respecto a otra. Se pueden restar números enteros, números con decimales, números negativos, e incluso pueden hacerse restas de fracciones, vectores, funciones y matrices. La resta es lo contrario a la suma. La resta no sigue la propiedad conmutativa, lo que quiere decir que si se cambia el orden de los factores, sí que se altera el resultado final, en concreto el signo positivo o negativo. Tampoco la propiedad asociativa, por lo que cuando se restan más de dos números, sí que importa el orden en el que se realiza la resta.

Practicar ejercicios de restas y problemas de restas es una de las mejores maneras para aprender a realizar esta operación de matemáticas. Además, existen herramientas que facilitan la resolución de sustracciones, una de las tareas numéricas más simples, como la calculadora de restas. De hecho, las restas con números muy pequeños es accesible para los niños, para que se adentren así en el mundo de las matemáticas y consiguen aprender a restar de manera adecuada • Minuendo: es el primer número de la operación, al que se le resta otro número. • Sustraendo: es el segundo número de la operación, que resta al primer número. • Diferencia: es el resultado de la resta. • Signo: es el signo, llamado menos, que se representa con una rayita pequeña (-).

MULTIPLICACIÓN

Multiplicación es un término con origen en el latín multiplicatio que permite nombrar el hecho y las consecuencias de multiplicarse o de multiplicar (incrementar el número de cosas que pertenecen a un mismo grupo).

Para la matemática, la multiplicación consiste en una operación de composición que requiere sumar reiteradamente un número de acuerdo a la cantidad de veces indicada por otro. Los números que intervienen en la multiplicación reciben el nombre de factores, mientras que el resultado se denomina producto. El objetivo de la operación, por lo tanto, es hallar el producto de dos factores.

La Multiplicación es un término con origen en el latín multiplicatio que permite nombrar el hecho y las consecuencias de multiplicarse o de multiplicar (incrementar el número de cosas que pertenecen a un mismo grupo).

Para la matemática, la multiplicación consiste en una operación de composición que requiere sumar reiteradamente un número de acuerdo a la cantidad de veces indicada por otro. Los números que intervienen en la multiplicación reciben el nombre de factores, mientras que el resultado se denomina producto. El objetivo de la operación, por lo tanto, es hallar el producto de dos factores. Cada factor, por otra parte, tiene su propia denominación: la cifra a sumar repetidamente es el multiplicando, mientras que el número que indica la cantidad de veces que hay que sumar el multiplicando es el multiplicador. La multiplicación, en definitiva, consiste en tomar el multiplicando y sumarlo tantas veces como unidades contiene el multiplicador.

DIVISION

La división es la operación matemática inversa a la multiplicación. Cosiste en encontrar cuántas veces está contenido un número en otro.

TÉRMINOS DE LA DIVISIÓN

1.- Dividendo,

2.- Divisor,

3.- Cociente y

4.- Resto.

LAS OPERACIONES CON CONJUNTOS

Las operaciones con conjuntos

El álgebra de conjuntos, nos permiten realizar operaciones con conjuntos y obtener como resultado otro conjunto.

Centraremos nuestro estudio en las siguientes: unión, intersección, diferencia, diferencia simétrica y complemento.

Para obtener una mejor comprensión, necesitamos en primer lugar conocer adecuadamente la teoría de conjuntos, que encontramos desarrollada en el siguiente artículo.

Determinación de un conjunto

Un conjunto se puede determinar de dos maneras: por extensión y por comprensión.

Por extensión:

Un conjunto está determinado por extensión cuando se escriben uno a uno todos sus elementos. Para ello los escribimos cada elemento separados por comas y encerrados entre llaves. Por ejemplo, el conjunto de los números naturales menores que 9: A = {1,2,3,4,5,6,7,8}

Por comprensión:

Un conjunto está determinado por comprensión cuando solamente se menciona una característica común de todos los elementos. Por ejemplo, el conjunto formado por las letras vocales del abecedario: B = {x / x es una letra vocal}. Dos conjuntos son idénticos si, y sólo si, contienen los mismos elementos.

Unión de conjuntos

La unión de dos conjuntos A y B se define como el conjunto de todos los elementos que están en el conjunto A o en el conjunto B. La unión de dos conjuntos de denota como A ∪ B. También, se puede escribir como A ∪ B = {x|x∈A o x∈B}

Es decir que al unir dos conjuntos, el resultado contiene a todos los elementos de ambos conjuntos.

Además en la unión de conjuntos se cumple las siguientes propiedades:Conmutativa: por lo tanto A ∪ B = B ∪ A

Asociativa: es decir que dados tres o mas conjuntos tendremos (A ∪ B) ∪ C = A ∪ (B ∪ C)

Intersección de conjuntos

Realizar la intersección de dos o más conjuntos, es definir un nuevo conjunto formado solamente por aquellos elementos que estén presentes en todos los conjuntos en cuestión. En otras palabras: sólo forman parte del nuevo conjunto, los elementos que tengan en común.

Existe un símbolo matemático para la intersección: ∩, como el símbolo unión invertido.

Para poner un ejemplo,la intersección de dos conjuntos llamados G y H se denota de la siguiente manera: G ∩ H.

        Diferencia de conjuntos

Operación en la cual dos conjuntos, A y B, especifican cuales elementos de uno no están en el otro, formando un nuevo conjunto llamado diferencia. La diferencia del conjunto A y el conjunto B, se representa como: A-B. La diferencia del conjunto B y el conjunto A, se representa como: B-A. Ambas operaciones arrojan resultados distintos, cuando los conjuntos no son iguales.

En la diferencia de conjuntos se cumple las siguientes propiedades: la diferencia de conjuntos no es asociativa, y no es conmutativa.

La diferencia es distributiva con respecto a la unión: (R ∪ S) – T = (R – T) ∪ (S – T); y a la intersección de conjuntos: (R ∩ S) – T = (R – T) ∩ (S – T).

      Diferencia simétrica de conjuntos

Dados dos conjuntos A y B, su diferencia simétrica, A Δ B, es un conjunto que contiene los elementos de A y los de B, menos los que son comunes a ambos.

En la diferencia simétrica de conjuntos se cumple las siguientes propiedades:Asociativa: (A Δ B) Δ C = A Δ (B Δ C)

Conmutativa: A Δ B = B Δ A

Distributiva respecto a la intersección: A ∩ (B Δ C) = (A ∩ B) Δ (A ∩ C).

Complemento de conjuntos

Para trabajar el complemento de conjuntos debemos recordar que existen conjuntos universales. Éstos son los que tienen todos los elementos de una clase, es decir que se usa como referencia para formar otros conjuntos, y se representa con la letra U.

El complemento de un conjunto A se forma con los elementos que le hacen falta al conjunto A para ser igual al conjunto universal. Esto de representa con Ac. Luego Ac = U – A

El complemento de conjuntos cumple las siguientes propiedades:

• Puesto que el conjunto universal contiene todos los elementos en consideración, y el conjunto vacío no contiene a ninguno, es decir: Uc = ∅
• El complemento del complemento de A es el propio A: (Ac)c = A
• La unión de un conjunto y su complementario es el conjunto universal: A ∪ Ac = U
• Un conjunto y su complementario son disjuntos: A ∩ Ac = ∅
• El complementario de A está contenido en el complementario de cualquier subconjunto de A: B ⊆ A implica que Ac ⊆ Bc.