😊PLANO CARTECIANO MAS FACIL QUE NUNCA 😱😱💖

Que es el  Plano cartesiano

Se conoce como plano cartesiano, coordenadas cartesianas o sistema cartesiano, a dos rectas numéricas perpendiculares, una horizontal y otra vertical, que se cortan en un punto llamado origen o punto cero.

La finalidad del plano cartesiano es describir la posición o ubicación de un punto en el plano, la cual está representada por el sistema de coordenadas.

El plano cartesiano también sirve para analizar matemáticamente figuras geométricas como la parábola, la hipérbole, la línea, la circunferencia y la elipse, las cuales forman parte de la geometría analítica.

Elementos del plano cartesiano

Los elementos y características que conforman el plano cartesiano son los ejes coordenados, el origen, los cuadrantes y las coordenadas. A continuación, te explicamos cada uno.

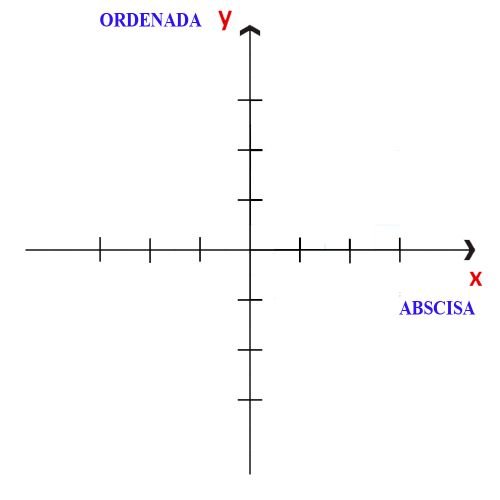
Se llaman ejes coordenados a las dos rectas perpendiculares que se interconectan en un punto del plano. Estas rectas reciben el nombre de abscisa y ordenada.Abscisa: el eje de las abscisas está dispuesto de manera horizontal y se identifica con la letra “x”.

Ordenada: el eje de las ordenadas está orientado verticalmente y se representa con la letra “y”.

Origen o punto 0

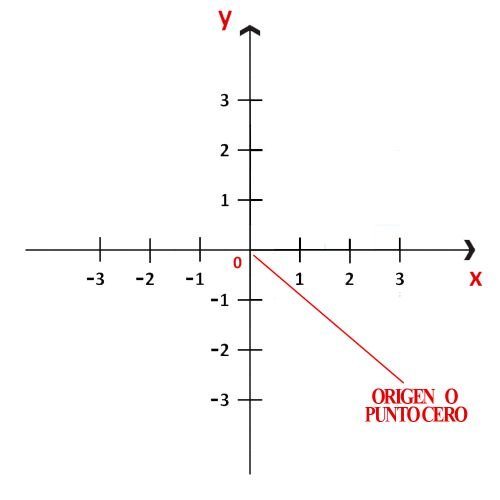
Se llama origen al punto en el que se intersecan los ejes “x” y “y”, punto al cual se le asigna el valor de cero (0). Por ese motivo, también se conoce como punto cero (punto 0). Cada eje representa una escala numérica que será positiva o negativa de acuerdo a su dirección respecto del origen.

Así, respecto del origen o punto 0, el segmento derecho del eje “x” es positivo, mientras que el izquierdo es negativo. Consecuentemente, el segmento ascendente del eje “y” es positivo, mientras que el segmento descendente es negativo.

Cuadrantes del plano cartesiano

Se llama cuadrantes a las cuatro áreas que se forman por la unión de las dos rectas perpendiculares. Los puntos del plano se describen dentro de estos cuadrantes.

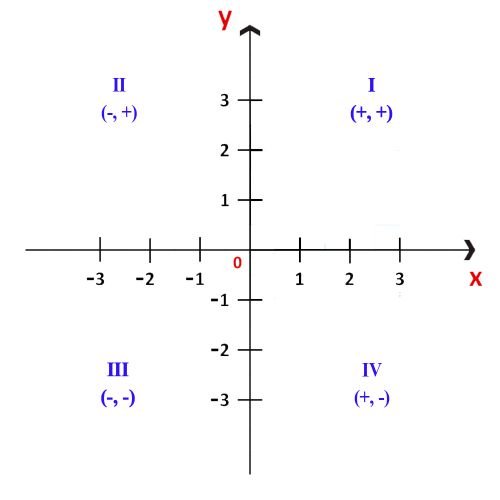
Los cuadrantes se enumeran tradicionalmente con números romanos: I, II, III y IV.

Cuadrante I: la abscisa y la ordenada son positivas.

Cuadrante II: la abscisa es negativa y la ordenada positiva.

Cuadrante III: tanto la abscisa como la ordenada son negativas.

Cuadrante IV: la abscisa es positiva y el ordenada negativa.

Coordenadas del plano cartesiano

Las coordenadas son los números que nos dan la ubicación del punto en el plano. Las coordenadas se forman asignando un determinado valor al eje “x” y otro valor al eje “y”. Esto se representa de la siguiente manera:

P (x, y), donde:

• P = punto en el plano;
• x = eje de la abscisa (horizontal);
• y = eje de la ordenada (vertical).

Si queremos saber las coordenadas de un punto en el plano, trazamos una línea perpendicular desde el punto P hasta el eje “x” –a esta línea la llamaremos proyección (ortogonal) del punto P sobre el eje “x”.

Seguidamente, trazamos otra línea desde el punto P hasta el eje “y” –es decir, una proyección del punto P sobre el eje “y”.

En cada uno de los cruces de las proyecciones con ambos ejes, se refleja un número (positivo o negativo). Esos números son las coordenadas.

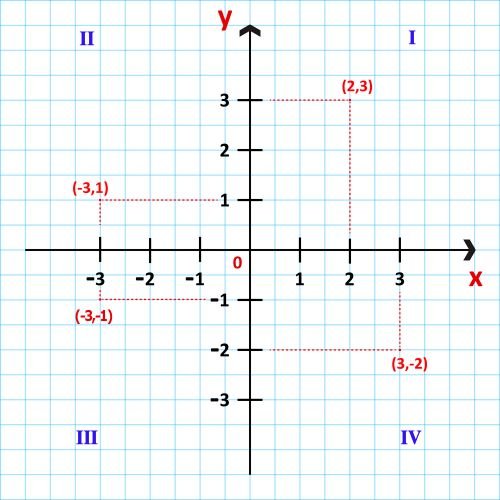
En este ejemplo, las coordenadas de los puntos en cada cuadrante son:

• cuadrante I, P (2, 3);
• cuadrante II, P (-3, 1);
• cuadrante III, P (-3, -1) 
• cuadrante IV, P (3, -2).

Si lo que queremos es saber la ubicación de un punto a partir de unas coordenadas previamente asignadas, entonces trazamos una línea perpendicular desde el número indicado de la abscisa, y otra desde el número de la ordenada. 

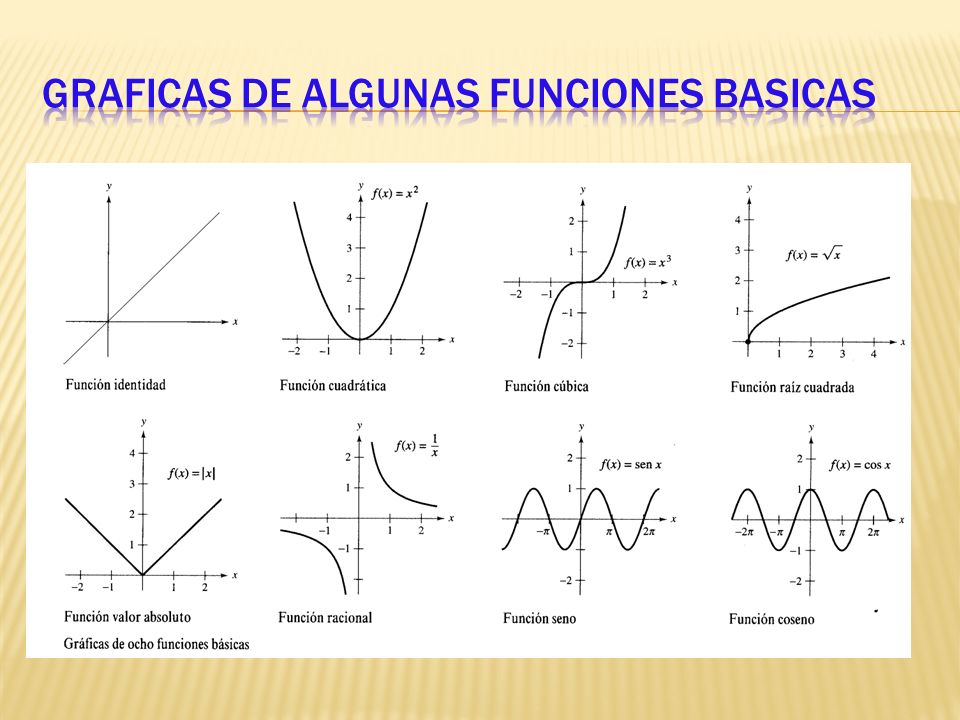
Funciones en un plano cartesiano

Una función representada como: f(x)=y es una operación para obtener de un variable independiente (dominio) las variables dependientes (contra dominio). Por ejemplo: f(x)=3x

La relación del dominio y el contra dominio es biunívoca, lo que significa que tiene solo dos puntos correctos.

Para encontrar la función en un plano cartesiano se debe primero tabular, o sea, ordenar los puntos en una tabla las parejas encontradas para posicionarlas o ubicarlas después en el plano cartesiano.